Golden Logo
When I retired I thought I was done with business cards, but I still wanted a card I could give to people with my contact details. But every business card Iíve seen has the companyís logo, and even if Iím not an employee anymore I wanted a nice logo. So I drew on my creativity, and recycled a graphic design Iíd done already, my Proof of Pythagoras painting (more on that below). It was shades of gray and square, not ascetically pleasing as a logo, so changes were called for. I needed something taller than wide, but how tall? I decided to extend the golden ratio that Iíd used for the shape of my Proof of Pythagoras triangles, and made a golden-ratio rectangle standing tall, with my Proof of Pythagoras diagram in the top square. So I had my card template:

Celebrating my 50 years in science
The background color of my logo is gold, extending the golden ratio idea to the traditional color for a fiftieth, golden anniversary. The bookends of my 50 years in science are two very different publications, in 1965 and 2015:
D. G. Lee and D. T. Johnson; THE CHROMIC ACID OXIDATION OF 2-PROPANOL IN TRIFLUOROACETIC ACID. Can. J. Chem. 43, 1952 (1965).
Johnson NP, Johnson DT, Kirkeeide RL,et al; Repeatability of fractional flow reserve despite variations in systemic and coronary hemodynamics. J Am Coll Cardiol Intv 2015;8: 1018Ė27.
My coauthor status in both these is due to the generosity of the lead authors. In 1965 I was a high school student, employed by the chemistry professor at Camrose Lutheran College as a lab assistant, and that job itself an unexpected opportunity for me as a young science whiz. He helped jump-start my career in science, although I didnít go on to study chemistry in university. As an undergraduate I studied physics, with enough geophysics to get a job in mining exploration after graduation. I like to say that on the job I learned geophysics from the ground up, from wielding an ax in the bush of Canadaís north to doing airborne electromagnetic surveys.
After 5 years in mining exploration I went back to graduate school in computing science, with a Masterís thesis in artificial intelligence on ďDecision Theory and Automatic PlanningĒ (1977). Then with Suncor, I worked in technical computing on mining oil sands, and on to a stint as a planning and economics analyst, again learning diverse skills on the job. I moved to Amoco, an oil company in Houston, as a geophysicist again, shifting to seismic methods from electromagnetics, and then again to integrating geophysics and reservoir engineering. This all gave plenty of scope for my scientific orientation, more directed to business objectives than academic publications, although I am proud of my one sole-author paper, ďUnderstanding air-gun bubble behavoirĒ in Geophysics v59#11 (1994). I retired from the company, now BP, in 2008 (and again from contract work there in 2010 and 2011). Iím no longer paid for scientific work, but now volunteer as a research assistant for our son Nils Johnson, a cardiologist at the University of Texas, who got me working on coronary pressure tracings in 2013. Both he and my first scientific mentor Don Lee are much more focused scientists, compared to my eclectic efforts bracketed by the two publications 50 years apart.
Links to publications:
D. G. Lee and D. T. Johnson, 1965: http://www.nrcresearchpress.com/doi/pdfplus/10.1139/v65-261
Daniel T. Johnson, 1994: http://geophysics.geoscienceworld.org/content/59/11/1729.abstract;
full text requires membership
Johnson NP, Johnson DT, Kirkeeide RL,et al, 2015: http://www.sciencedirect.com/science/article/pii/S1936879815006998;
use free PDF download, not Purchase
Master of Science
Over the years Iíve had many job titles on business cards, variations of geophysicist, analyst, and supervisor. So I wondered how to describe myself on my new card, and settled on the broad-brush Master of Science, since I do indeed have a diploma from a highly regarded university certifying me as that. My wife likes to say I took this title because Master of the Universe was already taken (by financial pretenders, Iíd say). If I were blue collar, I could say jack of all trades, master of none, but as a techie I think Iím more like a jack of some sciences, would-be master of all.
Golden logo construction
A Master of Science must love mathematics, and so I have to say something about the golden ratio. Wikipedia is the place I go for background on almost anything, so hereís a link: https://en.wikipedia.org/wiki/Golden_ratio. The idea is that (a+b) is to a as a is to b, so the ratio a/b is about 1.618. A golden rectangle makes a square and a smaller golden rectangle:
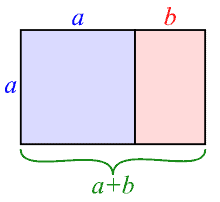 Note that a and b
are used differently here than in my Pythagoras notes below.
Note that a and b
are used differently here than in my Pythagoras notes below.
Wikipedia also explains the traditional connection of gold with a 50-year celebration, often a wedding anniversary, see https://en.wikipedia.org/wiki/Wedding_anniversary.
In plane geometry, some figures can be constructed with only compass and straight edge, and the development of mathematics through history involves proving which figures can be and which canít. I didnít pay much attention to this when I first chose the golden ratio for my Proof of Pythagoras painting or for my Golden Logo, but then I realized I could actually do the construction:
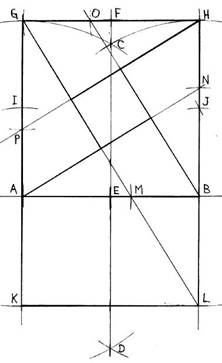
I wonít belabor this story with the details, but leave it as an exercise to the reader to follow the steps.
Proof of Pythagoras, notes from 2006
Diane and I aren't sure just when or how we came up with the idea of a painting using white on white, but perhaps it was a visit to the Rothko Chapel and his paintings in black.† But it was only that much of an idea when we saw a 48 by 36 inch canvas on sale and bought it.† And then it sat in our storeroom for over a year, a concrete but very occasional reminder of our idea.† Each time we'd ask ourselves what sort of painting we'd like, and all we agreed on was that it should be geometric, especially with our love of the art of M. C. Escher.† But wish as we might, inspiration didn't come.
Then on March 24, 2006, I was reading the Wall Street Journal at lunch and saw on the front page a diagram headed "Pythagoras's theorem a2 + b2 = c2 (From the Encyclopedia Britannica entry for 'Pythagoras')" and showing a square subdivided into two smaller squares and two rectangles each with a diagonal to make right triangles with sides labeled a, b, and c (see Appendix).† The text of the article, about the relative merits of the Encyclopedia Britannica and Wikipedia, didn't provide further explanation, and I was left wondering how the diagram demonstrated the theorem. I couldn't see the idea behind the diagram, but afterward in my office I tried to remember how to prove the theorem, and whether I could recall or construct a simple diagram that would prove the theorem.† Inspired by the diagram in the article, I started to sketch diagrams with 4 triangles in a square, and quickly came up with a diagram like this:
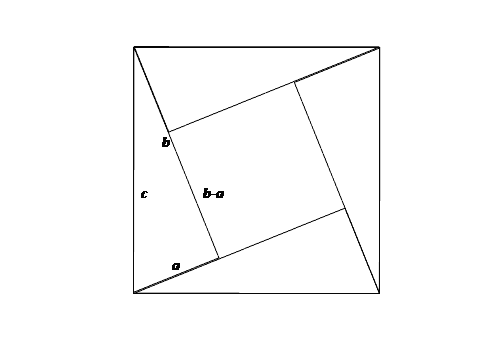
With the formula for the area of right triangles, ab/2, four of them plus the area of the small square, (b-a)2, make the area of the big square, c2.† Then a little algebra gives:
4
(ab/2) + (b-a)2 = c2
2ab +
b2 -2ab +† a2 = c2
b2 +† a2 = c2† Q.E.D.
So before lunch hour was over, I had come up with a diagrammatic proof of Pythagoras, one I couldn't recall seeing before.† I did recall that I'd first seen the proof of this theorem as the culmination of my Grade 10 geometry class, after weeks of working through Euclid, and to my dim memory much more difficult than this nice diagram.† So I knew that a simple proof existed, and I recall that I'd heard that there were many known proofs of this famous theorem, so I didn't expect that my own proof would be a new discovery.†
But I still
couldn't "see" the proof for the Wall Street Journal diagram, so I
went to the new authority, or at least newly accessible authority,
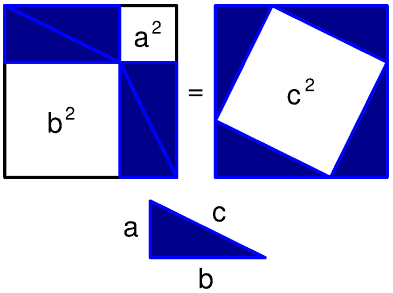
Wikipedia.† The article on "Pythagorean theorem" had a similar diagram
under the heading "Visual proofs." but with a second diagram that
made it obvious (see Appendix), rearranging the triangles within the original
square to leave a square with side c, rather than the original
squares of sides a and b.† A stunningly simple proof, no algebra
required.† So I was disappointed not to
have "seen" the proof at first, but also critical of the Wall Street
Journal for publishing half a proof of Pythagoras, with no further explanation.† Later at home I checked my copy of Encyclopedia
Britannica, to find the source the Wall Street Journal cited.† It wasn't there, another shortcoming of the
newspaper article which didn't say which edition of Britannica they were
referring to.
How this connected with our back burner
white art idea I don't know, but later the same day I told Diane that I thought
we finally had a concept, and told the story of my discovery and the idea to
paint the Proof of Pythagoras in white on white.† I'm not sure how I came up with the title for
the painting, but it seemed so natural, even if not the only possibility.† I was immediately keen on Pythagoras as
symbolic of the deeper meaning of geometry, mathematics and numbers, and recall
saying "What better proof to show than one you discover
yourself."† So I searched Google for
"Proof of Pythagoras" and found http://www.cut-the-knot.org/pythagoras/,
which catalogs the many known proofs of the theorem, including mine as #3 of 69
(many more trivial variations are also noted).†
I was pleased to learn I was in good company with many others through
history who have independently discovered ways to prove this famous and
fundamental theorem.
Turning this concept into a specific
design for our painting begged many questions:†
how big relative to the canvas, how to orient it, the shape of the
triangles which also determines the size of the small square, whether the small
ends of the triangles should point clockwise or counterclockwise, and how to
select shades and textures of white for the parts of the painting, what paint
and brushes and method to use.† My first
step toward a specific design was to experiment on the computer.† I used a program written in C to produce a
Postscript file, drawing a 3:4 shaded outline (the proportions of our canvas)
and four right triangles with variable shapes and shading (included in the
Appendix).† The C code is dated April 3,
so this happened quite soon after the concept.†
The shape of the triangle is determined by a single parameter, the
length of one of the sides, since the length of the hypotenuse is fixed by the
size of the large square.† I tried
different values and looked at the displays to see what looked good, and
thought it should be like baby bear's porridge, leaving a central square that
was not too big and not too small.
Then I had another idea, asking myself if
there was some ideal mathematical number I could use to nail down the broad
aesthetic choice.† The Golden Ratio came
immediately to mind, and I incorporated this in my display code with a pleasing
result when the two shorter sides of the triangle (which meet to make the right
angle) are in the golden ratio of about 1:1.62, which then also has the side of
the central square in the golden ratio with the short side, 0.62:1.† In fact, this is the defining feature of the
golden ratio, that (r-1) : 1 equals 1:r, so r
is the root of the quadratic equation r2 - r - 1 = 0,
close to but not exactly 1.62.† The
golden ratio isn't a necessary choice for my Proof of Pythagoras diagram, but
it does bring in another symbolic element to build on the numerological
mystique of Pythagorean philosophy.†
From the first I used only two different
shades of gray to distinguish the four triangles, the minimum needed, and left
the central square the same shade as the outline background.† Diane and I considered other possibilities,
but we both liked that simple plan, and decided that placing the darker
triangles on left and right looked better, rather than top and bottom, so
that's what we settled on.
That was early April, and with our
daughter Britta's wedding on April 22 everything went on the back burner
again.† And it was a good chance to let
this all ferment in our subconscious.†
After the wedding we started to consider paints, and bought some artist's
brushes at Texas Art Supply.† It seemed
acrylic paint would be convenient, and then I realized that premium latex house
paint was also acrylic, but we couldn't make up our minds whether it was
properly artistic, and that hesitance meant more delay.† Finally on the July 4 holiday weekend I was
eager to get on with it, and hauled down the canvas from the storeroom to lay
out the design on it.† The technique for
that had contributed to the delay also, but I decided that measuring and
marking directly on the canvas with light pencil lines would be fine, since I
could paint over the lines well enough.†
I used an Excel spreadsheet to calculate lengths in millimeters (762 mm
square), and devised a measuring sequence to ensure right angles and symmetry,
and to test and adjust for small measuring errors.† The pencil work went well, and made me keen
to get the paint.
I bought a quart of Pratt & Lambert
Accolade latex, off-white in a satin finish (midway between flat and gloss),
thinking to test it and see if it should be the darker shade or the lighter
before getting the other two.† Thinking
it might be on the light side, I painted the bottom triangle, but when dry on a
larger area than the paint chip it seemed clear that it could be the darker
shade, and that if we bought a clean white for the background I could mix the
two and get an intermediate lighter shade for the top and bottom
triangles.† So then it was set, and it
only took a few hours over two days to finish applying two coats of paint to
all the areas.† I tried to paint just up
to the pencil line from each side, deliberately leaving a remnant of it
visible.† This helped keep a sharp guide
line, but also leaves the finished painting with a clear indication of
technique, obviously done by hand when looked at up close.† I finished, titled, and signed my Proof of
Pythagoras painting and hung it in its long-intended spot over our fireplace on
July 4, 2006 (see photo below).† And I
decided I needed to top it off by writing these notes before memory fades.
Daniel T. Johnson, Houston, TX,
2006-Jul-09

Appendix to
Proof of Pythagoras notes
Wall Street Journal diagram
from 2006-Mar-24, page A1 (front page)

Visual proof of Pythagoras
from Wikipedia article on
"Pythagorean theorem"
C program to draw my proof
void godraw()
{
†††††† int i;
†††††† float
as,aa,ab,ac,af;
†††††† if(pot==NULL)
return;
†††††† as=3000.;
†††††† ac=1.0;
†††††† //ab=ac*0.5;
†††††† ab=ac*sqrt(2.)/sqrt(sqrt(5.)+5.);
†††††† aa=sqrt(ac*ac-ab*ab);
†††††† printf("%f
%f %f %f\n",aa,ab,ac,ab/aa);
†††††† pf("%!PS");
†††††† pf(".12
.12 scale % assume 600 dpi");
†††††† //pf("1
1.11 scale");
†††††† pf("5
setlinewidth");
†††††† pf("/point
{.12 div} def");
†††††† pf("/s90
{90 rotate show -90 rotate} def");
†††††† //pf(".9
.9 .9 setrgbcolor");
†††††† pf("
900† 900 moveto");
†††††† pf("4500† 900 lineto");
†††††† pf("4500
5700 lineto");
†††††† pf(" 900
5700 lineto");
†††††† pf("closepath
gsave");
†††††† af=0.85;
†††††† fprintf(pot,"%f
%f %f setrgbcolor fill\n",af,af,af);
†††††† pf("grestore
stroke");
†††††† pf("2700
3300 translate gsave");
†††††† for(i=0;i<4;++i){
††††††††††††† fprintf(pot,"%f
%f translate\n",-0.5*as*ac,-0.5*as*ac);
††††††††††††† pf("0
0 moveto");
††††††††††††† fprintf(pot,"%f
0 lineto\n",as*ac);
††††††††††††† fprintf(pot,"%f
%f lineto\n",as*aa*aa/ac,as*aa*ab/ac);
††††††††††††† pf("closepath
gsave");
††††††††††††† af=0.80-0.05*(i%2);
††††††††††††† fprintf(pot,"%f
%f %f setrgbcolor fill\n",af,af,af);
††††††††††††† pf("grestore
"); //pop from gsave, set up for stroke
††††††††††††† pf("grestore
90 rotate gsave");
†††††† }
†††††† if(pot){
††††††††††††† pf("showpage");
††††††††††††† fclose(pot);
††††††††††††† pot=NULL;
†††††† }
}
